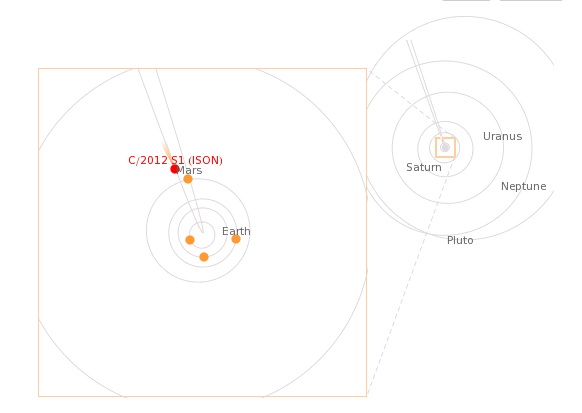
Comet Ison passing Mars (Wolfram Alpha)
I just got back from the Black Forest Star Party where Dr. Carey Lisse, head of NASA’s ISON Observing Campaign, gave a speech on comet ISON.
Comet ISON (see [1], [2]) is passing by Mars soon (Oct 1) and it will be “grazing the sun” before the end of the year, so I wondered if there was some relationship between the orbital period of a planet and the time it takes a passing comet to go from the planet to the Sun. Turns out there is a relationship. Here’s the approximate rule:
Time to sun $\approx$ Orbital Period / $ 3 \pi \sqrt{2} \approx $ Orbital Period / 13.3 !
In the case of ISON and Mars,
Time to sun $\approx$ 687 days / 13.3 $\approx$ 52 days.
But Oct 1 + 52 days is Nov 22, and perihelion is on Nov 28. Why so far off?
Well, turns out that Mars is farther from the sun than usual. If we correct for that, then the formula estimates perihelion to within 1 day—much better.
For those that like derivations, here is the derivation for the 13.3 rule.
The orbital period of a planet is $T_p = 2 \pi \sqrt{ r^3 \over {G m_S} }$ where $m_S$ is the mass of the Sun, $r$ is the radius of the planet’s orbit (or, more precisely, the semi-major axis of its orbit), and G = 6.67e-11 is the gravitational constant.
The speed of a comet from the Oort cloud is derived from its energy.
Kinetic Energy = -Potential Energy
$ \frac12 m v^2 = G m m_S / r$
$v = \sqrt{ {2 G m_S}\over{r}} $
where $r$ is the distance from the comet to the sun.
So the time for a Sun grazer to go from distance $r_0$ to the sun is about
$$T_S = \int_0^{r_0} {1\over v} dr $$
$$ = \int_0^{r_0} \sqrt{ r\over{2 G m_S}} dr $$
$$ = \frac13 \sqrt{ 2 r^3 \over{G m_S} }.$$
Finally,
$$T_p/T_S = {{2 \pi \sqrt{ r^3 \over {G m_S} }}\over{ \frac13 \sqrt{ 2 r^3 \over{G m_S} }}} = 3 \pi \sqrt{2} \approx 13.3.$$
Related Posts via Categories
-
This is so cool!
Comments are now closed.
2 comments